3. Shallow Neural Network

시작에 앞 서…

이 글은 Coursera의 Neural Networks and Deep Learning Deep 수업을 정리한 자료입니다.
교수님의 말씀을 잘 이해하지 못한 부분도 있으니, 수업을 들으시면 더욱 좋을 것 같습니다.

• Week1 : Introduction Deep Learning
• Week2 : Neural Networks Basics
• Week3 : Shallow Neural Network
• Week4 : Deep Neural Network

Neural Networks Overview

이제 본격적으로, neural network(신경망, 이하 NN)에 대해서 공부할 차레입니다. 시작에 앞서 간략한 overview가 진행됩니다. 왜 지난 시간에 Logistic regression을 배웠을까요? Logistic regression이 각각의 neuron을 담당하기 때문입니다. neuron이 중첩되어 표시된다는 것은, logistic regression이 중첩되어 구성된다는 뜻이 됩니다. 이러한 중접을 구분하기 위해서, layer로 묶게 됩니다. 각각의 layer는 brackets[]을 이용하여 구분하게 됩니다.

Neural Network Representation

NN의 명칭 및 구조에 대해서 살펴봅니다. NN은 input layer, hidden layer, output layer로 구성됩니다. input layer는 data인 X를 뜻합니다. hidden layer는 neuron에 의해 data를 가공하는 layer들을 뜻합니다. 마지막 결과값은 output layer에 의해서 도출되게 됩니다. input layer는 어떤 data의 가공이나 연산이 필요 없으므로, 통상 input layer를 제외한 나머지 layer로 그 NN의 정의합니다. 2-layer NN 이라고 하면, 하나의 hidden layer와 output layer로 만들어진 NN을 일컫습니다. 그 외에 눈여겨 볼 사항으로는, w 의 크기입니다. logistic regression에서는 features의 수에 의해 결정되었지만, NN에서는 거기에 neuron의 수 만큼 더 필요하게 됩니다. 즉, 이전에는 하나의 w 만 처리했다면, 이젠 neuron의 수 * hidden layer의 수 만큼의 w 를 관리하게 된 셈입니다. 거기에 따라, b 의 값도 neuron의 수 만큼 구해질 수 밖에 없겠죠.

Computing a Neural Network’s Output

그럼, 어떻게 해야 output layer의 값을 구할 수 있을까요?

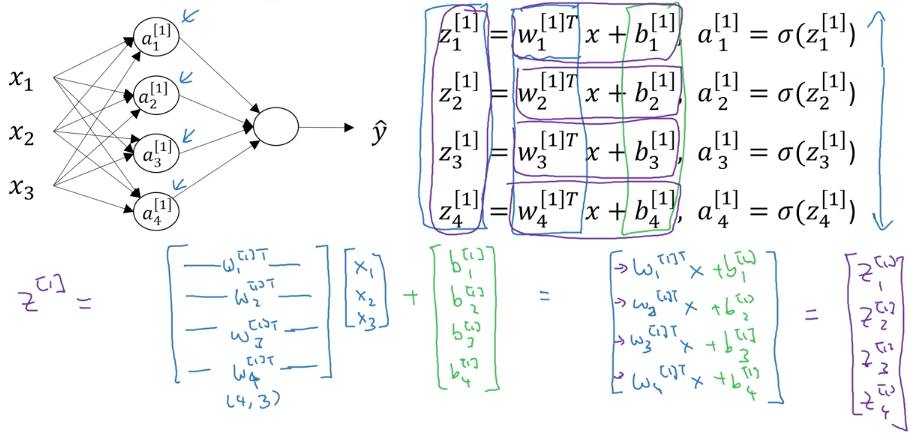
먼저, hidden layer에 대한 계산을 진행해야 합니다. 각각이 logistic regression으로 구성되어 있고, 4개의 neuron으로 되어 있으므로, 4번을 수행해야 합니다. 보기만 해도 꽤 복잡해 보입니다. 거기다가 feature가 증가되면, 눈으로 확인하기도 어려울 것 같습니다. 하지만, 지난 시간에 배운 Vectorizing을 적용하면, 아래와 같이 간단하게 정의할 수 있습니다.

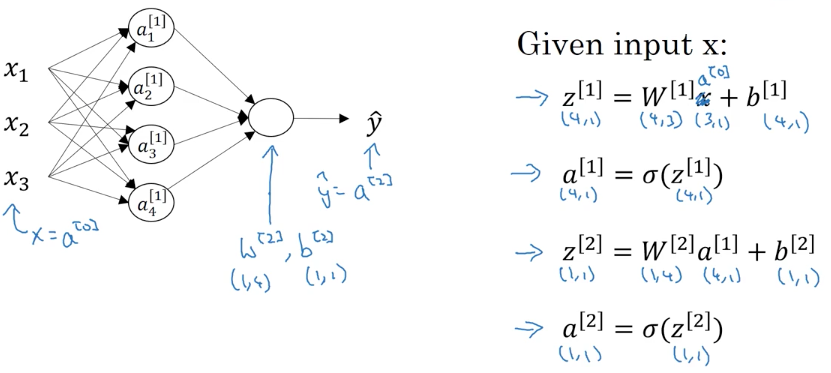
위의 4줄이면, output을 값인 a[2] 를 구할 수 있습니다. 간단하죠.

Vectorizing across multiple examples

아까까지, 살펴본 방법은 어디까지 하나의 x 에 대한 알고리즘이었습니다. 하지만, 현실은 전혀 그렇지가 않습니다. 수 많은 m(통상, data의 수)이 우리에겐 기다리고 있죠. 일반적인 방법은 for-loop를 이용해서, m번 수행하는 것이 있겠습니다. 물론, 그렇게 하지 않겠죠. Vectorization이 성능이 훨씬 좋으니까, 당연히 Matrix Multiplication(행렬곱)을 적극적으로 이용해야 합니다.

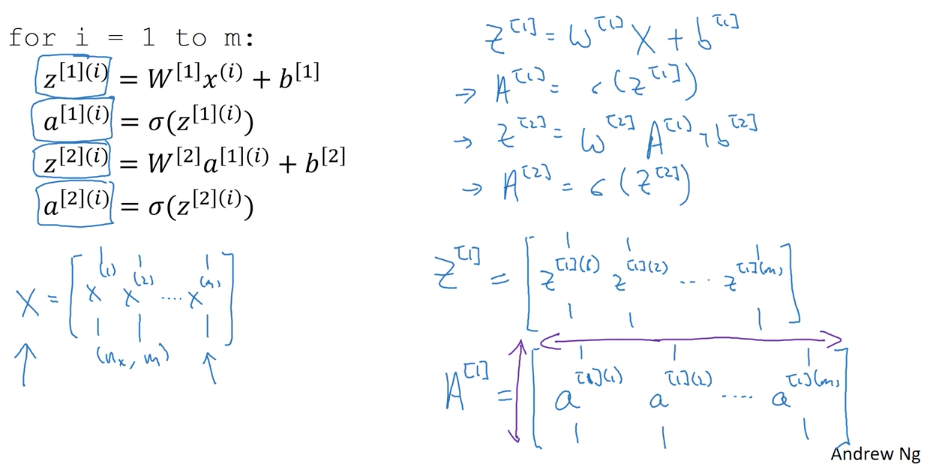
대문자를 이용해서 행렬 전체를 뜻하도록 변경한 것 외에는, 아까와 크게 달라진게 없어 보입니다. 이렇게 간결하게 표현할 수 있다니 경외감마저 드네요. 혹시, 이해가 가지 않는 분들을 위해서, Explanation for Vectorized Implementation에서 이 부분에 대해서 부연을 해 주십니다.

Activation functions

Activation function이 뭘까요? 앞에서 각 node의 결과값인 a 를 구할 때 사용한 Sigmoid 함수가 그 예가 됩니다. Activation function에는 아래와 같은 종류가 있습니다.

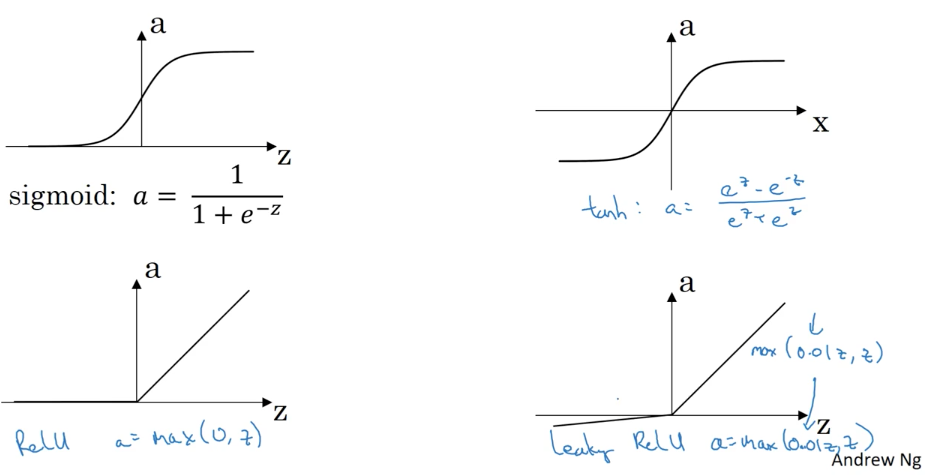
Activation function이 중요한 이유는, Gradient descent(경사하강법)을 적용할 때에 성능에 직접적인 영향을 주기 때문입니다. 기억하시겠지만, slope(기울기)를 가지고 하강을 하기 때문에 증감에 쉬운 기울기를 반환하는 activation function이 당연히 빠른 성능을 보장하게 됩니다. 각각의 장단점을 살펴보겠습니다.

• Sigmoid : {0 <= a <= 1}, tanh가 더욱 좋은 성능을 보여주기 때문에 거의 사용하지 않습니다. 예외적으로 output layer에서는 사용됩니다.
• tanh : { -1 <= a <= 1}, Sigmoid를 변환(shifted)한 함수로 대부분의 경우 Sigmoid보다 좋은 성능을 보여줍니다. 이는 z가 0에 가까울 때, 0.5보다는 0을 반환하는 것이 다음 hidden layer에 쉽게 처리되기 때문입니다.
• ReLU : max(0, z) Sigmoid와 tanh는 z의 값이 매우 크거나 작은 경우에 slope의 값이 0에 가까워지므로 gradient descent 성능을 저하시키게 됩니다. 이를 개선한 함수로 가장 많이 사용됩니다.
• Leaky ReLU : max(0.01*z, z) 으로 ReLU가 0의 값을 반환하는 점을 개선한 버전입니다. 어떤 사람들은 더 좋은 성능을 보여준다고 하지만, 언제나 그런 것은 아닌 것 같습니다.

그렇다면, 우리는 항상 ReLU를 선택해야 할까요? 교수님께서는, 모든 알고리즘을 시도해 보길 권하십니다. 그것이 NN Architecture 를 공고히 하는 일이며, 그런 상황에서 미래에 대한 대응도 더욱 쉬울 것이라고 합니다.

Why do you need non-linear activation functions?

꼭, activation function을 사용해야 하는 걸까요? activation function이 없다면, NN은 단순히 linear regression으로 정리될 수 있습니다. 왜냐하면, hidden layer가 얼마나 있던지, w에 반영될 수 있으므로 hidden layer는 없는 것과 마찬가지가 됩니다. 다만, output value가 수치인 경우에는 linear activation function을 마지막 node에서 사용할 수 있습니다. 물론, 이런 경우에도 hidden layer에는 ReLU 혹은 tanh가 activation function으로 사용되어야만 합니다.

Derivatives of activation functions

앞서 정리한 4가지 activation function의 미분값을 구합니다.

• Sigmoid : g’(z) = a(1 - a)

이건 지난 주에 이미 살펴 보았습니다. 미분을 해보면 어렵지 않게 구해집니다.

• tanh : g’(z) = 1 - a^2

이것도 미분 공식만 기억하시면 쉽게 도출 가능합니다.(혹시, 궁금하신 분들을 위해서 Derivative of tanh)

• ReLU : g’(z) = 0 if z < 0 , 1 if z >= 0

사실, 미분 가능하지 않기에 교수님도 undefine이라는 표현을 중간에 사용하셨습니다만, slope를 구하기 위함이니 이용할 수만 있으면 됩니다. Leaky ReLU는 0 대신에 0.01을 반환하면 되겠습니다.

Gradient descent for Neural Networks

NN에서 Gradient descent를 어떻게 사용하는지 살펴봅니다. 앞서 보았던 output value를 구하는 과정은 forward propagation에 해당합니다. 거기서 한발 더 나아가 w 와 b 를 수정할 수 있도록 Gradient descent를 적용할 것 입니다. 지난 주에 보았던 것 처럼, Gradient descent를 적용하기 위해서는 dw와 db의 값을 구해야 합니다. 그리고 NN에서는 w와 b 값이 layer의 수 만큼 있기 때문에, 각각의 layer를 달리 구해야 할 것입니다. 이러한 과정을 back propagation(역전파)라고 합니다.

보시는 것 처럼, back propagation에 더욱 구할 내용이 많습니다. 다음 영상에서 각각에 대해 조금 더 자세하게 살펴 봅니다.

Backpropagation intuition (optional)

지난 주에 보았던, Logistic Regression으로 설명을 시작합니다. 두 번째 보아서 그런지 꽤 직관적입니다. 그걸 확장하여 2 layer NN을 살펴 봅니다. output -> hidden layer로 향하는 과정은 Logistic Regression과 동일합니다. hidden -> input layer로 진행되는 과정은 조금 더 복잡합니다. 그 중에서 가장 중요한 부분은 바로, dz[1] 을 구하는 방법입니다. dz[2] 의 경우에는 a[2] - y와 같이 간단하게 구할 수 있었습니다만, 다음 layer의 값을 바탕으로 구해야 하기 때문입니다.

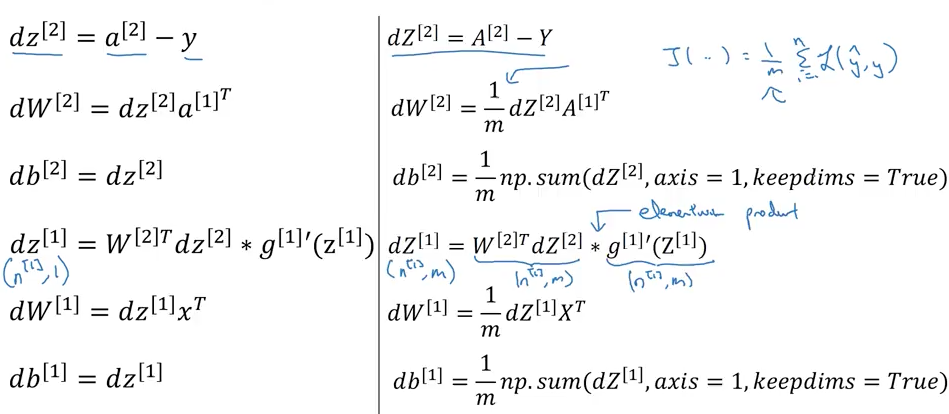
Random Initialization

파라미터의 초기값에 대한 내용입니다. w 와 b 에 해당하는데, 0으로 초기값을 설정하게 되면 여러 hidden layer가 있다고 할지라도, 제대로 작동되지 않는다고 합니다. 당연한게, w[2]T * a[2] + b[2] 의 경우에, 0과의 곱이므로 사실상 의미없는 노드로 전락하게 됩니다. 따라서, random한 초기값으로 w를 설정할 필요가 있습니다. 거기에 아주 작은 수로 설정하는게, 전체적인 성능에 좋다고 합니다. activation function이 잘 작동하기 위해서는 0에 가까운 작은 값이, gradient descent에서 효과적인 slope(기울기)를 반환하기 때문입니다.