시작에 앞 서…

이 글은 Coursera의 Neural Networks and Deep Learning Deep 수업을 정리한 자료입니다.
교수님의 말씀을 잘 이해하지 못한 부분도 있으니, 수업을 들으시면 더욱 좋을 것 같습니다.

Week1 : Introduction Deep Learning

Week2 : Neural Networks Basics

Week3 : Shallow Neural Network

Week4 : Deep Neural Network

아주 방대한 neural network을 만들기 위해서는, 아주 얕은 neural network(shallow neural network)를 만들 수 있어야 합니다. 그러기 위해서는 logistric regression(로지스틱 회귀)를 제대로 이해해야 합니다.

Logistic Regression as a Neural Network

Binary Classification

Binary Classification이란, 0과 1 처럼, discrete value을 결과로 보여주는 경우를 뜻 합니다. “맞아? 아니야?” 이런 질문도 사실, binary classification의 하나입니다. 혹은, “고양이? 아닌가?”라는 질문도 마찬가지입니다. 고양이에 대한 질문은, 사진을 바탕으로 판단하게 되는데 사진을 어떻게 데이타로 표현할 수 있을까요? 파일 이름이라도 맞춰나 되나 싶지만, machine learning에서는 모든 것을 matrix(행렬)로 표현합니다. 사진의 크기가 $64 \times 64$ 이라면, 데이타의 feature는 4098개로 이루어졌다고 보는 거죠. 각 픽셀을 RGB의 3가지 값으로 표현하게 되면, 12288개로 이루어지게 됩니다. 그런 사진이 10만장을 가지고 있다면, $(12288, 100000)$ 이라는 커다란 matrix가 만들어지고, 이를 input data를 뜻하는 $X$ 라고 합니다. 이렇게 준비된 10만장의 사진이 다 고양이면 안되겠죠. 각각의 사진이 고양이인지 아닌지를 알려주어야 합니다. 이렇게 결과를 label이라고 하며, $Y$ 라는 label matrix로 표현합니다. $Y$ 는 $(1,100000)$ 의 크기를 가집니다. 그 외에도 여러 표기법들이 있습니다. 이런 symbol을 사용하면, 단순한 표기가 가능하다는 장점이 있으나, 모르면 도통 알 수 없다는 단점도 있죠.

Logistic Regression

logisitic regression(로지스틱 회귀)를 배울 차례입니다. logistic regression은 binary classificiation의 하나입니다. 즉, 0과 1이라는 결과를 보여줍니다. 본격 설명에 앞서, notation을 좀 더 보고 가도록 하겠습니다.

$X$ : input data matrix, 크기는 $(\text{# of features} \times \text{# of data})$
$Y$ : label data matrix, 크기는 $(1 \times \text{# of data})$
$x_{(i)} \in X$ : $X$ 에서 $i^{th}$ 번째 column vector를 의미합니다. matrix는 대문자로 표현하고, column vector(개별 컬럼)을 소문자로 표현합니다.
$m$ : # of data, $X$ 의 컬럼의 수에 해당합니다.
$n$ : # of features, 하나의 input data가 포함하는 세부 값들을 feature라 합니다. $x$ 는 $n$ 차원의 값을 가지므로 $x \in \mathbb{R}_{n}$ 로 표현합니다.

그럼, Logisric Regression은 어떻게 구할 수 있을까요? 다음의 식을 사용합니다.

$\hat{y} = \sigma (w^T x + b) \tag 1$

$\hat{y}$ : $y$ 가 아니라, $\hat{y}$ 인 이유는 예측치이기 떄문입니다.
$w$ : 각 x의 features와 연산되어질 파라미터입니다.
$b$ : threshold라 하여, x와 상관없이 적용될 보정치가 됩니다.
$\sigma$ : sigmoid(시그모이드 함수)로, $\sigma = \frac{1}{1+e^{-x}}$ 으로 정의됩니다. 이런 함수를 쓰는 이유는, y의 값을 0~1사이로 만들기 위함입니다.

machine learning은 training과 testing 나누어집니다. training은 말 그대로, 훈련을 시키는 건데요, 위의 $w, b$ 를 찾는 과정을 뜻합니다. 그리고 testing을 $\hat{y}$ 의 정확도를 검증하는 과정입니다. (1)의 식에서 구해야 할 값은 바로 $w, b$ 인 셈입니다.

Logistic Regression Cost Function

학습을 하고 예측을 하는 것만큼 중요한 일이, 얼마나 잘 맞는가입니다. 이를 cost라고 표현하는데, 연산 비용이라기 보다는 오류 비용이라고 보시면 더욱 이해가 쉽겠습니다. 당연한 이야기지만, 얼마나 맞는지 예측하기 위해서는 오차를 구하면 됩니다. 오차라는 건, 예측과 실제의 차입니다. 이렇게 개별 오차를 구하는 함수를 cost function 혹은 loss function이라 합니다.

$L(\hat{y}, y) = \hat{y} - y$

간단하지만, 문제가 있습니다. 오차의 합을 구할 때, 음수 오차와 양수 오차가 상쇄될 수 있습니다. 그리고 $0 <= \hat{y} <= 1$ 의 작은 값이라, 오차가 제대로 반영되지 않을 수도 있습니다. 따라서 다음의 함수를 사용합니다.

$L(\hat{y}, y) = -\{ y\log(\hat{y}) + (1-y)\log(1-\hat{y}) \}$

$\log$ 는 오차를 증폭하는 역활을 하고, 음수 오차의 문제도 해결되었습니다.

Gradient Descent

Gradient Descent(경사하강법)은, 최적의 파라미터를 구하기 위한 방법입니다. 앞서, logistic regression의 파라미터가 w와 b라고 하였습니다. 이 파라미터를 어떻게 구할 것인가가 관건이 되겠습니다. 대표적인 방법으로 경사하강법이 있는데, 이는 미분을 통하여 빠르게 값을 줄이는 방향을 찾기 위함입니다. 아까 L(a, y)가 개별 data에 대한 내용이라면, J(w, b)는 전체 Loss의 평균치가 됩니다.

Gradient Descent

우측 하단에 보이는 그래프가 J(w, b)가 되겠습니다. 이 함수의 최소값이 되는 순간은 아래로 볼록(Convex)한 부분인 경우이고, 미분을 한다면 수렴할 수 있는 곳이기도 합니다. 우측에 빨간선으로 그린 그래프들은, local optimum에 대한 이야기입니다. Convex가 하나만 존재하지 않는다면, global optimum을 찾기란 어렵습니다. 미분이 수렴하였지만, 여기가 최적인지는 알 수가 없는 상태가 됩니다. 이런 경우, 초기값이 중요해 지는데, 여러 차례 random initial value를 통해, 최적의 optimum을 탐색해야만 합니다.

Derivatives & More Derivative Examples

미분에 대한 강의가 이어집니다. 고교 수학 시간에 배운 내용이라, 특별히 다른 점도 없고 교수님께서 워낙 자세하게 설명해 주십니다.

Computation graph & Derivatives with a Computation Graph

Graph를 만들어서, back propagation을 간단하게 진행합니다. 이 back propagation을 위해서, 앞서 복습한 미분법을 사용할 차례입니다.

Logistic Regression Gradient Descent

이젠, 앞서 배웠던 J함수에 대해서도 미분을 적용할 차례입니다.

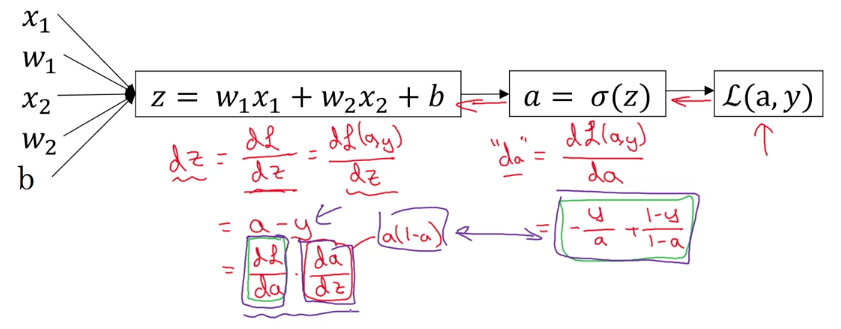
Logistic Regression Derivative

조금 복잡해 보이지만, 머리 속으로 J함수에 대한 미분과 sigmoid 함수에 대한 미분을 떠 올리시면 금방 이해할 수 있습니다. 혹시, sigmoid function에 대한 미분값은 도무지 모르겠다면, Derivative of sigmoid function σ(x)=1/1+e^−x을 참고 하시면, elegant한 증명을 보실 수 있습니다.

Gradient Descent on m Examples

이제 위의, 결과를 모든 data에 대해서 수행할 차례입니다.

Logistic Regression on m examples

Vectorization을 진행하기 전의 pseudo code라고 생각하시면 되겠습니다.

Python and Vectorization

Vectorization…

for-loop 보다 Matrix Multiplication(행렬곱, 이하, MM)이 더욱 빠르고 코드가 간결해질 수 있습니다. 아시다시피, MM의 경우 슈트라센 알고리즘과 같은 optimized algorithm을 사용하기 때문에, MM의 일반적인 구현에 가까운 for-loop의 복잡도 O(n^3)보다 당연히, 빠른 결과를 가져올 수 있습니다. MM을 적극적 활용하여 코드를 작성하는 것은 Vectorization이라 합니다.

Vectorizing Logistic Regression’s Gradient Output

Matrix를 사용하는 경우, 훨씬 간결한 코드를 실제적으로 보여줍니다. 특히, 행렬 관련 연산은 matlab이나 numpy에서 충분히 제공하고 있기 때문에, loop를 사용하지 않고도 충분히 표현할 수 있습니다.

by indices vs. by matrices

성능은 물론, 알고리즘 자체도 단순하게 표현되었습니다.

Broadcasting in Python

Python에서 행렬을 연산하는데, 제공되는 기능 중에 하나인 Broadcasting에 대해 설명합니다. 행렬의 곱이나 차를 구하기 위해서는, 각 행렬의 크기가 동일해야 합니다. Broadcasting은 하나의 행렬을 반복시켜, 크기가 다른 행렬도 연산이 될 수 있도록 제공되는 기능입니다. 무조건 수행되는 것은 아니고, 하기의 조건을 만족해야 합니다.

rank가 다른 경우, 1을 원소로 가지는 rank를 추가합니다.
각 차원의 크기가 동일하거나, 1인 경우에 연산이 가능합니다.
연산이 가능한 모든 차원에 대해서, Broadcasting이 일어납니다.
Broadcasting 후의 shape은 최대 크기로 결정됩니다.
특정 차원의 크기가 1이고 다른 차원이 1인 아닌 경우에, 다른 차원의 값이 복사됩니다.

A note on python/numpy vectors

python은 훌륭한 유연함을 제공하는 언어로, 적은 코드로도 강력한 표현이 가능하지만, 언어의 복잡도나 Broadcasting과 같은 기능을 제대로 이해하지 못한다면 애매한 버그나 이상한 결과가 나타날 수도 있습니다. 예를 들어,

rank 1 array : matrix가 아닌, list에 가깝습니다. shape로 찍어보면 (n,) 이라고 나오는데, row와 column을 가지는 matrix와 다릅니다.

가급적 애매하거나 오류를 내기 쉬운 구문은 사용하지 않는게 좋겠습니다.

Quick tour of Jupyter/iPython Notebooks

jupiter를 이용하면, 과제 제출은 물론 학습에도 편리하게 사용할 수 있습니다.

단축키는 Help > Keyboard Shortcuts 을 확인하시면 되겠습니다.

Explanation of logistic regression cost function

앞 서 배운, cost function이 어떻게 도출되었는지 다루는 optional lesson입니다. P(y|x)라는 확률로 접근하여, 도출하는데 생각보다 간단하고 흥미롭습니다.

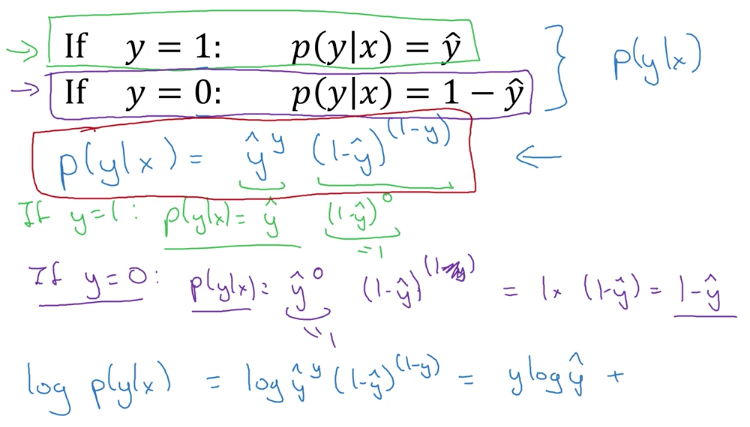
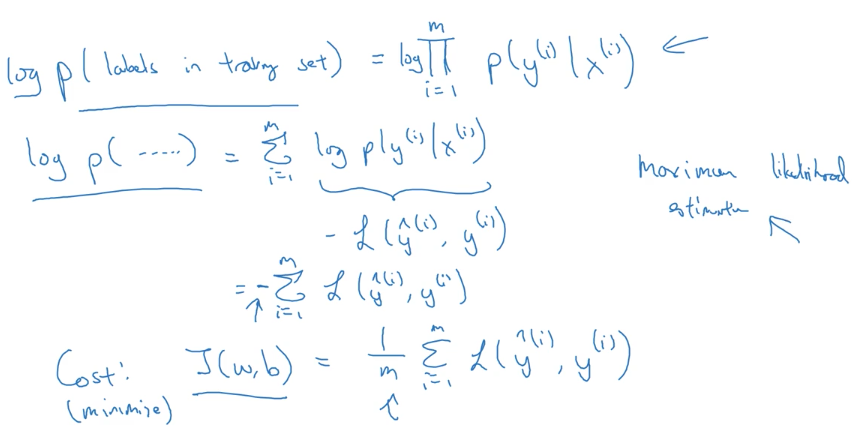
regression cost function

예전, machine learning 강좌에서는 여기까지 다루지 않았던 것 같은데, 새삼 분명해지는 기분이 드네요.