1. Practical Aspects of Deep Learning

시작에 앞 서…

이 글은 Coursera의 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization 수업을 정리한 자료입니다.
교수님의 말씀을 잘 이해하지 못한 부분도 있으니, 수업을 들으시면 더욱 좋을 것 같습니다.

• Week1 : Practical Aspects of Deep Learning
• Week2 : Optimization Algorithms
• Week3 : Hyperparameter tuning, Batch Normalization, and Programming Frameworks

이번 강의는 지난 강의에서 neural network을 더욱 심화하여 성능을 향상시키는 방법에 대해 다루고 있습니다. 그러기위해서 기초적인 몇 가지 개념들을 학습해야 할 필요가 있습니다. train/dev/test 셋들이나, bias와 variance에 대한 이해, 또 regularization에 대한 지식도 필요로 합니다. 그리고 몇 가지 실험적인 이슈를 다루는 것까지가 이번 주에 학습할 내용이 되겠습니다.

Setting up your Machine Learning Application

Train / Dev / Test sets

neural network과 같은 알고리즘은 훈련에 사용되는 데이타와 검증에 사용되는 데이타를 따로 구분해서 사용합니다. 만약, 훈련 과정에 사용된 데이타를 가지고 검증을 하려고 하면, 이미 $W$와 $b$ 값에 반영되었기 때문에 항상 좋은 결과만 보여주게 됩니다. 확보된 전체 데이타에서 각 역활에 맞게 나누어 사용하는데, 이를 train, dev 그리고 test set으로 구분합니다. train set 은 neural network을 훈련시키는데 사용되는 데이타입니다. neural network은 훈련된 사용된 데이타와 성능이 어느 정도 비례하기 때문에, 대부분의 데이타를 훈련에 할당합니다. 나머지 조금의 데이타만 남겨 두는데, 예를 들면 0.25%에 해당되는 데이타를 dev나 test로 활용합니다. 예전에는 dev(cross-validation) set 과 test set 을 구분하여, 알고리즘 자체에 대한 검증 dev set으로 진행하고, test set을 이용해서 정확도를 산출하였습니다. 설명에서 알 수 있듯이, dev와 test의 성격이 조금 겹치는 감이 있기에, 통합하여 사용하는 조직이 많다고 합니다.

Bias / Variance

Bias 와 Variance 는 성능을 진단하는 하나의 척도입니다. 그림을 보면 훨씬 직관적인데,

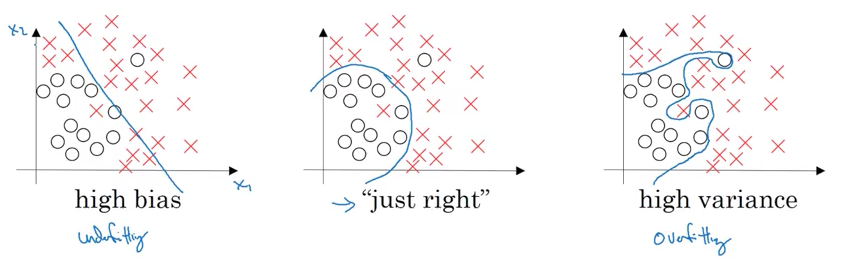
쉬운 이해를 위해 logistic regression으로 표현했고 좌측이 high bias인 상태이고, 우측이 high variance인 상황입니다. 좌측 그림은 O,X의 구분을 정확하게 가르기 보다는, 대충 간결한 직선으로 구분짓고 있습니다. 즉, bias 는 간략화하여 예측도가 나빠진 상황을 뜻합니다. 우측 그림의 경우는 지나치게 세세하게 구분하는 바람에 복잡하게 구분짓고 있습니다. 이는 high variance 인 상태로, 데이타의 복잡도나 노이즈가 그대로 반영되어 오히려 예측도 나빠지는 상황을 뜻합니다. 우측 그림의 세세한 구분 보다는, 중간 그림의 적절한 영역 구분이 예측도가 더 좋다는 뜻이 됩니다. neural network의 경우는 어떻게 진단을 할 수 있을까요? 그림을 그려서 판단해야 할까요? train error와 dev error를 비교하여 판단합니다. train set과 dev set의 error가 서로 다를텐데, 그 값간의 차이를 바탕으로 bias 와 variance를 진단하게 됩니다. bias 라면, train set을 제대로 반영하지 못했기 때문에 train error값이 상대적으로 높게 측정됩니다. variance 라면, train data는 잘 반영하지만 본 적이 없는 데이타의 경우 예측이 나쁘기에, dev error가 train error보다 높게 측정됩니다.

Basic Recipe for Machine Learning

앞 서 bias와 variance를 배웠는데, 그 다음에 우린 어떤 행동을 취해야 할까요? 일단, bias에서 시작합니다. bias는 train set도 제대로 반영하지 못하는 상태이기 때문에, 모델에 문제가 있을 가능성이 높습니다. hidden layer나 node를 조정하여 neural network을 더욱 크게 만든다거나, 훈련 과정을 늘리는 방법을 생각할 수 있습니다. 아니면 데이타를 잘 반영할 수 있는 다른 neural network architecture를 적용할 수도 있습니다. 이를 통해, bias를 낮추고 나면, variance를 확인할 차례입니다. variance는 더 많은 데이타를 통해 완화할 수 있습니다. 또한 정규화를 통해서 데이타의 편향을 조절할 수도 있습니다 이런 과정을 통해, low bias에 low variance인 상태의 최적의 알고리즘을 만들 수 있게 됩니다.

예전에는 bias와 variance가 trade-off 관계에 있었습니다. 하나를 높이면 하나가 줄어드는 그런 상태였으나, neural network에서는 한 쪽을 상쇄하지 않아도 다른 쪽은 효과적으로 제어할 수 있게 되었습니다. 예를 들면, 더 많은 데이타는 bias에 상관없이 variance를 낮출 수 있습니다. 혹은, 더 많은 hidden layer는 variance에 영향없이 bias를 낮출 수 있습니다.

Regularizing your neural network

Regularization

Overfitting을 제어하는 방법으로 소개된 Regularization은 cost function을 통해 적용됩니다. 이전 강의에서 살펴본 logistic regression의 cost function J는 다음과 같습니다.

$$J(w,b) = \frac 1 m \Sigma_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})$$

여기에, regularization을 적용하면,

$$J(w,b) = \frac 1 m \Sigma_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) \color{maroon}{ + \frac{\lambda}{2m} \| w \|_2^2 }$$ $$\| w \|_2^2 = \Sigma_{j=1}^{n_x} w_j^2 = W^T W \tag 1$$

즉, $J$를 구할 때 마다, $W^T W$을 구해서 반영한다는 뜻입니다. 여기서 사용한 (1)은 2차원의 Euclidean norm(유클리드 노름)으로 다루고 있기 때문에, L2 Regularization 이라 부릅니다. 물론, L1 Regularization도 있습니다.(1차원의 거리값으로 절대값의 합)

지금까지 logistic regression으로 보았습니다만, 이번에는 neural network을 기준으로 살펴보겠습니다.

$$J(w^{[1]},b^{[1]},...,w^{[l]},b^{[l]}) = \frac 1 m \Sigma_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) \color{maroon}{+ \frac{\lambda}{2m} \Sigma_{l=1}^L \| w_F^{[l]} \|^2}$$

$L$에서 알 수 있듯이, layer에 대한 처리가 추가되었습니다. 그리고 Frobenius Form을 사용한다는 점입니다. matrix norm 중에서 가장 일반적인 경우를 p-norm이라고 하는데, p가 2인 특별한 경우 Frobenius Form이라고 합니다. 아까와 같이 2랑 동일하나, matrix의 경우라 달리 표기한다고 생각하시면 되겠습니다. 이렇게 cost function을 구했다면, gradient descent에 반영할 차례입니다.

$$dw^{[l]} = \frac{1}{m} dz^{[l]} X^T \color{maroon}{ + \frac{\lambda}{m} W^{[l]}}$$

이러한 regularization을 weight decay라고도 합니다.

Why regularization reduces overfitting?

regularization이 overfiiting에 왜 도움이 될까요? 단서는 $J(W, b)$에 있습니다. regulization term이 추가되면서, $W$ 값이 영향을 받게 됩니다. regulization parameter가 큰 값이라면, 상대적으로 $L(\hat{y}^{(i)}, y^{(i)})$은 작은 값을 가지게 됩니다. 이는 연쇄적으로 $W$와 $b$을 작게 만들게 됩니다. 이 값을 이용하는 $z^{[l]}$값도 작아지게 됩니다.

Dropout Regularization

또 다른 regularization 방법인 dropout에 대해 배울 차례입니다. dropout은 특정 neuron을 생략하는 방법입니다. 앞의 regularization의 핵심은 $W$를 줄이는데 있었다면, 이제는 $W$에 계산되는 수를 줄이는데 있습니다.

keep-prob이라는 표현이 나오는데, 이는 neuron을 얼마나 보존할지에 대한 확률입니다. 1이라면, 전혀 dropout을 하지 않겠다는 뜻이겠죠. keep-pros을 통해서 행렬을 확률적으로 몇몇 element를 False 값을 가지게 만들고, 곱을 이용해서, 값을 0으로 만듭니다. 재밌는 점은, 거기에 다시 keep-pros를 나눈다는 점입니다. 이런 방식을 inverted dFalse 값을 가지게 만들고, 곱을 이용해서, 값을 0으로 만듭니다. 재밌는 점은, 거기에 다시 keep-pros를 나눈다는 점입니다. 이런 방식을 inverted dropout이라고 합니다. 그 외 기억해야 할 점은, dropout은 gradient descent마다 랜덤하게 초기화 하여 사용합니다. test set을 수행할 때는 dropout을 쓰지 않는다고 합니다. 랜덤한 선택으로 인해, noise가 더 발생된다고 하네요.

Understanding Dropout

Dropout이 regularization에 도움이 되는 이유는, 특정 입력을 소거함으로써 데이타를 전체적을 더 잘 반영하기 때문입니다. 일종의 shrink weights라고 표현하는데, 특별히 큰 값이나 noise가 많은 데이타를 제외시키는 역활을 합니다. 또한 각각의 layer마다 다른 keep-pros을 설정함으로써, 특별히 overfitting을 일으키기 쉬운 layer를 다루기 좋습니다. Computer Vision과 같이 입력이 큰 경우에는 거의 기본적으로 사용된다고 합니다. 그 외 영역에서는 굳이 data가 넘치는 경우가 아니라면 사용할 필요가 없을 것 같다고 하네요. 특히, $J$ 함수에 대해 없어진 node를 반영하기가 까다로워, ploting같은 debugging은 어렵다고 합니다.

Other regularization methods

Overfitting을 줄이기 위해서, data를 늘리는 방법이 있었습니다. data를 늘리는 방법도 하나의 regularization이 될 수 있습니다. 예를 들어, 사진을 늘리거나 변형하여 새로운 data를 만들 수 있습니다. 이를 data augmentation이라 합니다. Early Stopping이라는 방법도 있습니다. train set과 dev set의 $J$를 각각 구하여, 둘 다 가장 작은 값을 취하는 iteration을 찾는 방법입니다. 모든 data를 training하지 않기 때문에, lambda regularization보다는 효율적이지 않다고 생각됩니다.

Setting up your optimization problem

Normalizing inputs

Normalizing은 $X$의 값을 정제하여, 효과적으로 적용시킬 수 있도록 변환하는 과정입니다. 과정은2가지 단계로 이루어집니다.

$$\mu = \frac{1}{m}\Sigma_{i=1}^{m}X^{(i)}$$ $$X := X - \mu \tag{subtract mean}$$ $$\sigma^2 = \frac{1}{m}\Sigma_{i=1}^{m}X^{(i)^2}$$ $$X := X - \sigma^2 \tag{normalize variance}$$

1번째는 평균값으로 값을 조정하는 일입니다. 2차 평면으로 예를 들면, 원점으로 옮기는 일입니다. 2번째 단계에서는 분산을 반영합니다. 값들간의 차이가 적어 응집해 있는 값들을 분산시키는 역활을 합니다. test set에 적용할 때에는 train set에서 사용한 $\mu, \sigma^2$를 사용해야 합니다.

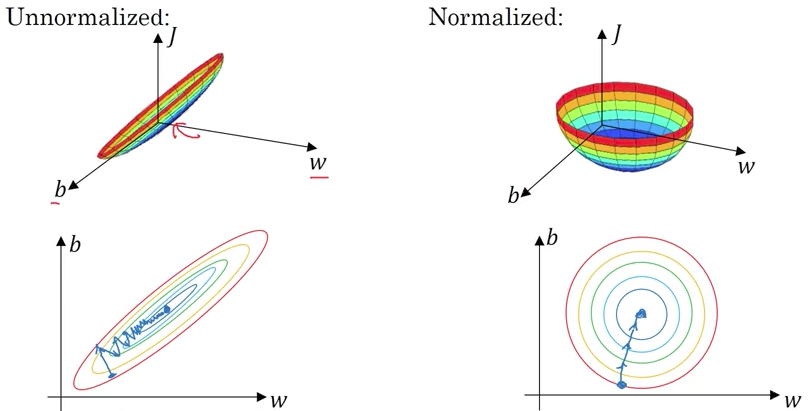
Normalizing의 역활은 위에 그림에서 알 수 있듯이, 값을 균형있게 나타낼 수 있다는 점입니다. 이는 gradient descent에서도 훨씬 이점이 있음을 하단의 그래프에서 알 수 있습니다.

Vanishing / Exploding gradients

neural network에서 발생하기 쉬운 문제 중에 하나는 $W$가 쉽게 너무 커지거나(exploding) 혹은 0에 가까워진다는(vanishing) 점입니다. 각각의 layer는 이전 layer의 곱으로 표현되는데, 이는 결과적으로 layer 수 만큼의 곱셈을 의미하게 됩니다. $W$의 초기값이 1에 근사하지 않으면 layer가 거듭될 수록 0에 수렴하거나 지수적인 증가를 나타내게 됩니다.

Weight Initialization for Deep Networks

Vanishing/Exploding을 완벽히 해결하는 방법은 없습니다. $W$의 초기값만 잘 설정된다면 Vashing/Exploding을 막을 수 있습니다. 초기값을 아래와 같이 설정합니다.

W[l] = np.random.randn(shape) * np.sqrt(2/n[l-1])

random한 값에, $\sqrt{\frac{2}{n^{[l-1]}}}$을 곱해줍니다. 이렇게 곱해주는 것은, $W^{[l]}$의 원소를 더욱 작은 값으로 만들어 $Z^{[l]}$의 원소가 1에 가까운 작은 값으로 만들기 위함입니다. 곱해지는 값은 activation function에 따라 조금씩 다릅니다. 위의 경우는, ReLU함수인 경우에 사용되며, $\tanh$의 경우에는 $\sqrt{\frac{1}{n^{[l-1]}}}$이나 $\sqrt{\frac{2}{n^{[l-1]+n^{[l]}}}}$을 사용합니다.

Numerical approximation of gradients

미분은 어떠한 점에서 기울기를 뜻합니다. 미분 공식을 기억해 보면,

$$f'(x) = \lim_{\epsilon\to0}\frac{f(x + \epsilon)}{\epsilon}$$

으로 $\epsilon$이 0에 수렴할 때의 기울기를 뜻합니다. 근사 미분은 그것보다 훨씬 단순합니다.

$$f'(x) \approx \frac{f(x + \epsilon)}{\epsilon}$$

일 때, $\epsilon$은 상대적으로 작은 값을 설정하면 됩니다. 여기서 조금 더 정확한 버전이 바로 two sided difference입니다.

$f'(x) \approx \frac{f(x + \epsilon) + f(x - \epsilon)}{2\epsilon}$ 다음 영상인, gradient checking에서 사용할 미분 근사 공식이 되겠습니다.

Gradient checking

backward propagation의 값을 확인하는 방법이 있다면, 디버깅은 물론 전체 개발 시간을 줄여줄 수 있습니다. 그러기 위해서는 비교할 대상이 있어야 하는데, 앞서 배운 미분 근사치를 비교하여 오차를 측정할 수 있습니다.

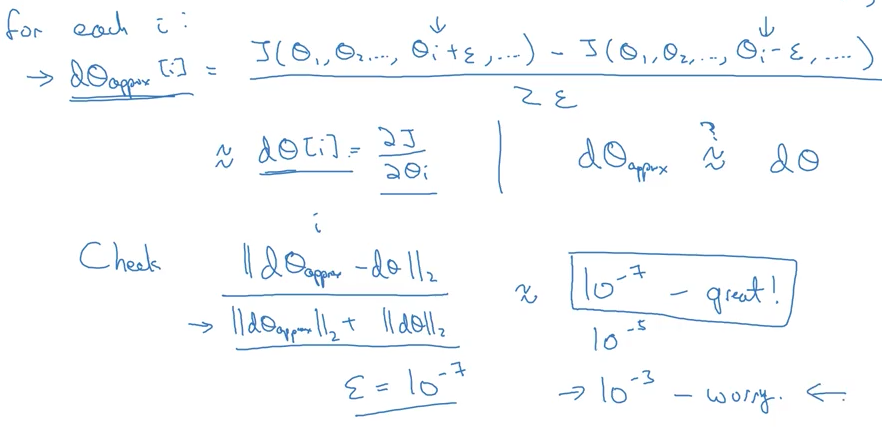
유클리드 거리를 구해서 오차가 $$10^{-7}^^이내라면, 상당히 훌륭한 수준입니다. 이렇게 점검하는 방법을 grad checking이라고 합니다.

Gradient Checking Implementation Notes

gradient checking을 적용하기 할 때, 몇 가지 주의 사항이 있습니다.

• debug에만 사용 : 미분 근사를 구하는 일은 상당히 느린 작업입니다. 학습(training)시에는 사용하지 않습니다.
• grad check가 실패하면 component를 확인 : 오차가 크게 발생했다면, 각각의 component를 비교해서, 문제되는 component를 찾아야 합니다. 그곳에 오류가 있을 가능성이 높으니까요.
• regulization : regularization을 사용한다면, $J$에 lambda 식이 더해지므로, 미분 근사치와 비교할 때 처리해 주어야 합니다.
• dropout 전에 검증 : dropout을 하게 되면, $J$함수가 쓰기가 무척 까다로워집니다. keep-pros는 1로 설정하고 grad checking을 진행한 후에, dropout를 진행하도록 합니다.
• random 초기화 : random 초기화를 하는 경우에는, 학습을 통해 $W, b$를 업데이트한 이후에 grad checking을 진행토록 합니다.